Mathematical Analysis of a Full Wave Rectifier

_{During the first half of each power cycle,}e_{2N is negative and} e_{1N is positive.} Therefore diode D1 conducts and current i1 flows through RL .This current is obtained as

i_{1=EmSinωt/(Rf+RL) = ImSinωt ( when 0≤ωt≤π)}

                                 = o   _{( when π ≤ωt≤2π)}

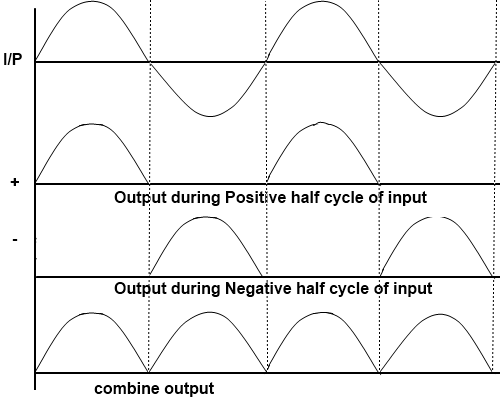
_{During the second half of each power cycle,}e_{2N is positive and} e_{1N is negative.} Therefore diode D2 conducts and current i2 flows through RL .This current is obtained as 

 i2_{=EmSinωt/(Rf+RL) = ImSinωt ( when}  π≤ωt≤2π)

                                 = o   _{( when 0≤ωt≤π)}

The current through the load is the sum of i1 and i2 and unidirectional in the whole cycle. The below figure shows the profile of currents  i1 and i2 and i. The  DC current is  

                  idc =1/2π [∫ ImSinωtd(ωt) + ∫ ImSinωtd(ωt) ] (first integral is integrated over o to π and second integral is integrated over π to 2π)

                           idc =  2Im/π

The rms current is given by

                             I =  [1/2π∫i²d(ωt)]^{0.5 (limit of the integration is from o to} 2π)

                               =   [1/2π∫I²mSin²ωtd(ωt)]^0.5

                                ⁼  Im/√2

It is seen that both Idc and  I in this circuit are twice of those in the half wave circuit.

The voltage across the load is (i_RL).

                         

Also

_{Vm  = EmRL/(Rf+RL}) 

Vdc = _EmRL/π_(Rf+RL)

V    = _EmRL/√2_(Rf+RL) 

The dc power delivered to the load is obtained as

                               P_dc = I² _dc*RL = 4E²_m*RL/π^²(Rf+RL)^²

^{The efficiency of Full Wave circuit is obtained as} 

                              P_in = I²(Rf+RL) = E²_m/2(Rf+RL)

The efficiency of the Full Wave rectifier , is obtained as 

                                        η = P_dc/ P_{in  = 0.812/}(1₊ Rf+RL)